Parastās frakcijas. Daļskaitļi, parastās daļskaitļi, definīcijas, apzīmējumi, piemēri, darbības ar daļskaitļiem Kur ir daļskaitļa skaitītājs un saucējs?

Frakcija matemātikā skaitlis, kas sastāv no vienas vai vairākām vienības daļām (daļdaļām). Daļskaitļi ir daļa no racionālo skaitļu lauka. Pamatojoties uz to rakstīšanas veidu, frakcijas tiek sadalītas 2 formātos: parasts veids un decimālzīme .

Daļas skaitītājs- skaitlis, kas parāda paņemto akciju skaitu (atrodas daļdaļas augšpusē - virs līnijas). Daļas saucējs- skaitlis, kas parāda, cik daļās vienība ir sadalīta (atrodas zem līnijas - apakšā). , savukārt, ir sadalīti: pareizi Un nepareizi, sajaukts Un salikts ir cieši saistīti ar mērvienībām. 1 metrs satur 100 cm, kas nozīmē, ka 1 m ir sadalīts 100 vienādās daļās. Tādējādi 1 cm = 1/100 m (viens centimetrs ir vienāds ar vienu simtdaļu no metra).

vai 3/5 (trīs piektdaļas), šeit 3 ​​ir skaitītājs, 5 ir saucējs. Ja skaitītājs ir mazāks par saucēju, tad daļa ir mazāka par vienu un tiek izsaukta pareizi:

Ja skaitītājs ir vienāds ar saucēju, daļa ir vienāda ar vienu. Ja skaitītājs ir lielāks par saucēju, daļa ir lielāka par vienu. Abos pēdējos gadījumos tiek izsaukta daļa nepareizi:

Lai izolētu lielāko veselo skaitli, kas ietverts nepareizā daļskaitlī, skaitītāju dala ar saucēju. Ja dalīšanu veic bez atlikuma, tad ņemtā nepareizā daļa ir vienāda ar koeficientu:

Ja dalīšanu veic ar atlikumu, tad (nepilnīgais) koeficients dod vēlamo veselo skaitli, un atlikums kļūst par daļdaļas skaitītāju; daļdaļas saucējs paliek nemainīgs.

Tiek izsaukts skaitlis, kurā ir vesels skaitlis un daļēja daļa sajaukts. Frakcija jaukts numurs var būt nepareiza frakcija. Tad jūs varat izvēlēties lielāko veselo skaitli no daļskaitļa un attēlot jaukto skaitli tā, lai daļdaļa kļūtu par pareizu daļskaitli (vai pazūd pavisam).

Mēs visu laiku dzīvē lietojam daļskaitļus. Piemēram, kad mēs ēdam kūku ar draugiem. Kūku var sadalīt 8 vienādās daļās vai 8 akcijas. Dalīties– Tā ir līdzvērtīga daļa no kaut kā veseluma. Četri draugi apēda kūkas gabalu. Formā matemātiski var ierakstīt četrus, kas ņemti no astoņiem gabaliem kopējā frakcija\(\frac(4)(8)\), tiek nolasīta daļa "četras astotdaļas" vai "četri dalīti ar astoņām". Tiek saukta arī parastā frakcija vienkāršā daļa.

Daļu josla aizstāj dalījumu:
\(4 \div 8 = \frac(4)(8)\)
Akcijas pierakstījām pa daļām. Burtiskā formā tas būs šādi:
\(\bf m \div n = \frac(m)(n)\)

4 – skaitītājs vai dividende, atrodas virs daļlīnijas un parāda, cik daļu vai akciju tika ņemtas no kopsummas.
8 – saucējs vai dalītājs, atrodas zem daļlīnijas un parāda kopējo daļu vai daļu skaitu.

Ja paskatīsimies vērīgi, tad redzēsim, ka draugi apēda pusi kūkas vai vienu daļu no divām. Rakstīsim to kā parastu daļskaitli \(\frac(1)(2)\, lasām “viena sekunde”.

Apskatīsim citu piemēru:
Ir laukums. Laukums tika sadalīts 5 vienādās daļās. Divas daļas tika nokrāsotas. Pierakstiet daļskaitli iekrāsotajām daļām? Pierakstīt daļu neēnotajām daļām?

Tika nokrāsotas divas daļas, un kopā ir piecas daļas, tāpēc daļa izskatīsies kā \(\frac(2)(5)\), lasāma kā “divas piektdaļas”.
Trīs daļas netika pārkrāsotas, kopā ir piecas daļas, tāpēc daļskaitli rakstām kā \(\frac(3)(5)\), daļskaitlis skan "trīs piektdaļas".

Sadalīsim kvadrātu mazākos kvadrātiņos un pierakstīsim daļskaitļus iekrāsotajām un neēnotajām daļām.

Ir 6 krāsotas detaļas, un kopā ir 25 detaļas. Mēs iegūstam daļskaitli \(\frac(6)(25)\), daļu nolasa “sešas divdesmit piektdaļas”.
Nepārkrāsotas ir 19 daļas, bet kopā 25 daļas. Mēs iegūstam daļskaitli \(\frac(19)(25)\), daļskaitlis skan "deviņpadsmit divdesmit piektdaļas".

Ir 4 pārkrāsotas daļas, un kopā ir 25 daļas. Mēs iegūstam daļskaitli \(\frac(4)(25)\), daļskaitlis skan "četras divdesmit piektdaļas".
Ir 21 daļa, kas nav pārkrāsota, bet tikai 25 daļas. Mēs iegūstam daļskaitli \(\frac(21)(25)\), daļskaitlis skan "divdesmit viena divdesmit piektā daļa".

Jebkuru naturālu skaitli var attēlot kā daļskaitli. Piemēram:

\(5 = \frac(5)(1)\)
\(\bf m = \frac(m) (1)\)

Jebkurš skaitlis dalās ar vienu, tāpēc šo skaitli var attēlot kā daļu.

Jautājumi par tēmu “kopējās frakcijas”:
Kas ir akcija?
Atbilde: dalīties– Tā ir līdzvērtīga daļa no kaut kā veseluma.

Ko rāda saucējs?
Atbilde: saucējs parāda, cik daļās vai daļās ir sadalīta kopsumma.

Ko rāda skaitītājs?
Atbilde: skaitītājs parāda, cik daļas vai akcijas tika paņemtas.

Ceļš bija 100 m. Miša nostaigāja 31m. Pierakstiet izteicienu kā daļu: cik tālu Miša ir gājis?
Atbilde:\(\frac(31)(100)\)

Kas ir parastā frakcija?
Atbilde: Kopējā daļa ir skaitītāja attiecība pret saucēju, kur skaitītājs ir mazāks par saucēju. Piemērs, parastās daļskaitļi \(\frac(1)(4), \frac(3)(7), \frac(5)(13), \frac(9)(11)…\)

Kā naturālu skaitli pārvērst parastā daļskaitlī?
Atbilde: jebkuru skaitli var uzrakstīt kā daļskaitli, piemēram, \(5 = \frac(5)(1)\)

1. uzdevums:
Nopirkām 2kg 700g melones. Viņi Mišai nogrieza \(\frac(2)(9)\) melones. Kāda ir sagrieztā gabala masa? Cik gramu melones ir palicis?

Risinājums:
Pārvērsim kilogramus gramos.
2kg = 2000g
2000g + 700g = 2700g kopējais melones svars.

Viņi Mišai nogrieza \(\frac(2)(9)\) melones. Saucējs satur skaitli 9, kas nozīmē, ka melone ir sadalīta 9 daļās.
2700: 9 = 300 g viena gabala svars.
Skaitītājā ir skaitlis 2, kas nozīmē, ka jums ir jāiedod Mišai divi gabali.
300 + 300 = 600 g vai 300 ⋅ 2 = 600 g ir tas, cik daudz melones Miša apēda.

Lai atrastu atlikušās melones masu, no kopējās melones masas ir jāatņem apēstā masa.
2700 - 600 = 2100 g melones pa kreisi.

Klase: 6

Mērķis: veido priekšstatu par daļskaitļa elementiem: skaitītāju, saucēju, daļskaitļu līniju.

Uzdevumi:

1. Apgūstiet kopējās datplūsmas elementus.
2. Attīstīt uzmanību un acis.
3. Izkopt kārtīgumu.

Aprīkojums:

• tabula "Parastās frakcijas";
• iestatīt "Akcijas un daļas";
• individuālas kartes.

Nodarbību laikā

I. Organizatoriskais moments.

Kāds numurs? Mēnesi? gads? Kurš mēnesis beidzās? Kāds tagad ir gada laiks? Ierakstiet datumu piezīmju grāmatiņā.

II. Mutiskais darbs.

1. Kā sadalīt 3 ābolus 2 cilvēkiem? 5 āboli uz 4 cilvēkiem? 2 āboli 3 personām?

Paskaidrojiet, kā iegūtas šīs frakcijas.

3. Strādājiet ar apli, kas sadalīts 4 daļās. Nosauc ceturtdaļu, divus ceturkšņus. Kā sauc 2 un 4, 1 un 4?

III. Jauna materiāla apgūšana.

1 ir skaitītājs, 4 ir saucējs.
2 ir skaitītājs, 4 ir saucējs.

Tā ir mūsu nodarbības tēma (stundas tēmas ierakstīšana piezīmju grāmatiņā).

• Skaitītājs, saucējs, daļrinda.

Tagad redzēsim, kā iegūt citas frakcijas. Mēs veidojam sloksnes uz tāfeles un piezīmju grāmatiņā. Sadaliet sloksnes 4 daļās un krāsojiet 2 daļās. Kāda ir frakcija?

Nosauc saucēju. Ko rāda saucējs?

Nosauciet skaitītāju. Ko rāda skaitītājs?

IV. Fiziskās audzināšanas brīdis(mūzikas pavadījumā).

V. Darba pie tēmas turpinājums.

Piezīmju grāmatiņas ieraksts:

3 – skaitītājs;
___ – daļskaitļu josla;
5 ir saucējs.

Pievēršam uzmanību pareizai vārdu “skaitītājs”, “saucējs”, “daļskaitļu līnija” pareizrakstībai uz tāfeles un tabulā “Parastās daļas”.

(Tiek izmantota zīme.)

Apskatīsim noteikumu par skaitītāju un saucēju.

Daļskaitļu josla ir dalījuma zīme.

Skolēniem tiek izsniegtas individuālas kartītes ar noteikumiem par skaitītāju un saucēju. Studenti izlasa noteikumu, pēc tam atkārto to skaļi korī.

VI. Konsolidācija.

Darbs pie atsevišķām kartēm.

Krāsojiet:

• 1 grupa - 3 šūnas.
• 2. grupa – 4 šūnas.
• 3. grupa – 6 šūnas.
• 4. grupa – 7. šūnas.

Izveidojiet to pašu taisnstūri savā piezīmju grāmatiņā un atzīmējiet daļu. Kurš uzdevumu izpilda ātrāk, strādā pie tāfeles ar komplektu “Akcijas un daļas”.

Rādīt: .

VII. Nodarbības kopsavilkums.

1. Ko tu studēji?
2. Ko rāda saucējs?
3. Kur tas ir ierakstīts?
4. Ko rāda skaitītājs?
5. Kur tas ir ierakstīts?
6. Skolēni tiek vērtēti.

VIII. Mājasdarbs. Uzziniet 2 noteikumus, izmantojot kartes.

Frakcija. Daļas skaitītājs un saucējs

1. definīcija. Daļa ir viena vai vairākas identiskas objekta daļas (daļas) vai kāda daudzuma.

Daļa tiek uzrakstīta, izmantojot divus naturālus skaitļus, no kuriem viens atrodas virs horizontālās līnijas, bet otrs zem tās.

2. definīcija. Tiek izsaukts numurs virs līnijas daļskaitļa skaitītājs. Tiek izsaukts numurs zem līnijas daļdaļas saucējs Skaitītāju un saucēju sauc par daļskaitļa vārdiem.

Saucējs daļskaitļu rāda cik ilgi mums ir vienādas daļas sadalīt objekts vai daudzums, un skaitītājs daļskaitļu rāda Cik daudz tādi paņemtās akcijas.

Piemēram, frakcija

kurā skaitītājs ir vienāds ar 8 un saucējs ir vienāds ar 17, nozīmē, ka mēs sadalām objektu vai daudzumu 17 vienādās daļās (daļās) un ņemam 8 šādas daļas.

1. piemērs. Klasē mācās 25 skolēni, daži apmeklē teātra pulciņu. Cik studentu apmeklē drāmas pulciņu?

Risinājums. Lai atrisinātu piemēru, jums jāsadala 25 studenti 5 daļās un jāņem 2 šādas daļas.

Atbilde . 10 skolēni.

2. piemērs. Pirmajā pārgājiena dienā tūrists veica paredzēto maršrutu, bet otrajā dienā - atlikušos 24 kilometrus. Cik kilometrus tūrists kopumā nostaigāja?

Risinājums. Viss maršruts ir sadalīts 7 vienādās daļās, no kurām 3 tūrists izbrauca pirmajā dienā (1. att.).

1 diena

1 diena

1 diena

2. diena

2. diena

2. diena

2. diena

1 diena

1 diena

1 diena

2 diena

2 diena

2 diena

2 diena

No 1. attēla redzams, ka 24 kilometri veido 4 no 7 maršruta daļām. Tātad 1 maršruta daļa ir vienāda ar

24: 4 = 6 (km),

un viss maršruts ir vienāds

Atbildi . 42 kilometri.

komentēt. Ja nav norādīts, no kāda objekta vai kāda izmēra daļa ņemta, tad tiek uzskatīts, ka daļa ņemta no skaitļa 1.

Jēdziens frakcija ir sinonīmi: vienkārša daļa, kopējā frakcija, racionālā daļa, daļskaitlis .

Pareizās un nepareizās frakcijas. Jaukti skaitļi

3. definīcija. Ja daļskaitļa skaitītājs ir mazāks par tā saucēju, to sauc pareiza frakcija. Citādi - nepareiza frakcija.

No šīs definīcijas jo īpaši izriet, ka pareizā daļa ir mazāka par vienu, bet nepareizā daļa ir lielāka par vienu vai vienāda ar vienu.

3. piemērs. - pareiza daļa un - nepareiza daļskaitļi.

Nepareizu daļskaitli vienmēr var izteikt kā vesela skaitļa un pareizas daļskaitļa summu. Šo operāciju sauc izceļot visu daļu no nepareizās daļskaitļa un tiek veikta, dalot ar atlikušo nepareizās daļskaitļa skaitītāju ar saucēju.

4. piemērs.

,

Skaitlis ir piemērs jaukts numurs. Veselu skaitli 2 un pareizu daļu sauc par veselu skaitli un jaukta skaitļa daļēja daļa attiecīgi.

Jebkuru jauktu skaitli vienmēr var pārvērst nepareizā daļskaitlī, piemēram,

Frakciju pamatīpašības, frakciju samazināšana, nereducējamā frakcija

Daļas galvenā īpašība zvaniet tālāk

Paziņojums, apgalvojums . Daļa kļūst par vienādu daļskaitli, ja tās skaitītāju un saucēju reizina vai dala ar to pašu skaitli.

4. definīcija. Tiek izsaukta darbība, kurā daļskaitļa skaitītājs un saucējs tiek dalīts ar vienu un to pašu skaitli samazinot daļu.

4. piemērs.

.

Mēs sāksim šīs tēmas izskatīšanu, izpētot daļskaitļa jēdzienu kopumā, kas sniegs mums pilnīgāku izpratni par parastās daļskaitļa nozīmi. Sniegsim pamatterminus un to definīciju, izpētīsim tēmu ģeometriskā interpretācijā, t.i. uz koordinātu līnijas, kā arī definējiet pamatoperāciju sarakstu ar daļskaitļiem.

Kopuma akcijas

Iedomāsimies objektu, kas sastāv no vairākām, pilnīgi vienādām daļām. Piemēram, tas varētu būt apelsīns, kas sastāv no vairākām identiskām šķēlītēm.

1. definīcija

Daļa no veseluma vai daļa- šī ir katra no vienādām daļām, kas veido visu objektu.

Acīmredzot akcijas var atšķirties. Lai skaidri izskaidrotu šo apgalvojumu, iedomājieties divus ābolus, no kuriem vienu sagriež divās vienādās daļās, bet otru četrās. Ir skaidrs, ka iegūto daiviņu izmērs dažādiem āboliem būs atšķirīgs.

Akcijām ir savi nosaukumi, kas ir atkarīgi no akciju skaita, kas veido visu objektu. Ja objektam ir divas daļas, tad katra no tām tiks definēta kā viena šī objekta otrā daļa; kad objekts sastāv no trim daļām, tad katra no tām ir viena trešdaļa un tā tālāk.

2. definīcija

Puse- viena otra objekta daļa.

Trešais– viena trešdaļa objekta daļu.

ceturksnis- viena ceturtā daļa no objekta.

Lai saīsinātu apzīmējumu, tika ieviesti šādi daļskaitļu apzīmējumi: puse - 1 2 vai 1/2; trešais - 1 3 vai 1/3; viena ceturtā daļa - 1 4 vai 1/4 un tā tālāk. Biežāk tiek izmantoti ieraksti ar horizontālu joslu.

Daļas jēdziens dabiski paplašinās no objektiem līdz daudzumiem. Tātad mazu objektu mērīšanai kā vienu no garuma vienībām var izmantot metra daļas (trešdaļu vai simtdaļu). Līdzīgi var piemērot arī citu daudzumu proporcijas.

Daļskaitļi, definīcijas un piemēri

Kopējās daļskaitļus izmanto, lai aprakstītu akciju skaitu. Apskatīsim vienkāršu piemēru, kas mūs tuvinās parastās daļskaitļa definīcijai.

Iedomāsimies apelsīnu, kas sastāv no 12 segmentiem. Katra daļa būs viena divpadsmitā daļa jeb 1/12. Divi sitieni – 2/12; trīs sitieni – 3/12 utt. Visi 12 sitieni vai vesels skaitlis izskatīsies šādi: 12/12. Katrs no piemērā izmantotajiem apzīmējumiem ir parastās daļskaitļa piemērs.

3. definīcija

Kopējā frakcija ir veidlapas ieraksts m n vai m/n, kur m un n ir jebkuri naturāli skaitļi.

Saskaņā ar šo definīciju parasto daļskaitļu piemēri ietver šādus ierakstus: 4/9, 11 34 917 54. Un šie ieraksti: 11 5, 1, 9 4, 3 nav parastas daļskaitļi.

Skaitītājs un saucējs

4. definīcija

Skaitītājs kopējā frakcija mn vai m/n ir naturālais skaitlis m.

Saucējs kopējā frakcija mn vai m/n ir naturālais skaitlis n.

Tie. Skaitītājs ir skaitlis, kas atrodas virs parastās daļdaļas rindas (vai pa kreisi no slīpsvītras), un saucējs ir skaitlis, kas atrodas zem līnijas (pa labi no slīpsvītras).

Ko nozīmē skaitītājs un saucējs? Parastās daļdaļas saucējs norāda, no cik daļām sastāv viens objekts, un skaitītājs sniedz informāciju par to, kāds ir attiecīgo daļu skaits. Piemēram, parastā daļa 7 54 mums norāda, ka noteikts objekts sastāv no 54 daļām, un par atlīdzību mēs paņēmām 7 šādas daļas.

Dabiskais skaitlis kā daļskaitlis ar saucēju 1

Kopējās daļskaitļa saucējs var būt vienāds ar vienu. Šajā gadījumā var teikt, ka attiecīgais objekts (daudzums) ir nedalāms un attēlo kaut ko veselu. Skaitītājs šādā daļskaitlī norādīs, cik šādu vienību tika paņemtas, t.i. formas m 1 parastajai daļai ir naturāla skaitļa m nozīme. Šis apgalvojums kalpo kā pamatojums vienādībai m 1 = m.

Pēdējo vienādību rakstīsim šādi: m = m 1 . Tas dos mums iespēju izmantot jebkuru naturālu skaitli kā parastu daļskaitli. Piemēram, skaitlis 74 ir parasts formas 74 1 daļskaitlis.

5. definīcija

Jebkuru naturālu skaitli m var uzrakstīt kā parastu daļskaitli, kur saucējs ir viens: m 1.

Savukārt jebkuru formas m 1 parasto daļskaitli var attēlot ar naturālu skaitli m.

Daļskaitļu josla kā dalījuma zīme

Iepriekš izmantotā objekta attēlošana n daļās nav nekas vairāk kā sadalīšana n vienādās daļās. Kad prece ir sadalīta n daļās, mums ir iespēja to sadalīt vienādi starp n cilvēkiem – katrs saņem savu daļu.

Gadījumā, ja mums sākotnēji ir m identiski objekti (katrs sadalīts n daļās), tad šos m objektus var vienādi sadalīt starp n cilvēkiem, piešķirot katram vienu daļu no katra no m objektiem. Šajā gadījumā katrai personai būs m daļas 1 n, un m daļas 1 n iegūs parasto daļu m n. Tāpēc daļu m n var izmantot, lai attēlotu m vienību sadalījumu starp n cilvēkiem.

Rezultātā iegūtais paziņojums izveido saikni starp parastajām daļskaitļiem un dalīšanu. Un šīs attiecības var izteikt šādi : Daļu līniju var domāt kā dalījuma zīmi, t.i. m/n = m:n.

Izmantojot parasto daļskaitli, mēs varam uzrakstīt divu naturālu skaitļu dalīšanas rezultātu. Piemēram, 7 ābolu dalījumu ar 10 cilvēkiem rakstām kā 7 10: katrs saņems septiņas desmitdaļas.

Vienādas un nevienādas parastās daļas

Loģiska darbība ir salīdzināt parastās daļskaitļus, jo ir skaidrs, ka, piemēram, ābola 1 8 atšķiras no 7 8.

Parasto daļskaitļu salīdzināšanas rezultāts var būt: vienāds vai nevienāds.

6. definīcija

Vienādas kopīgās frakcijas– parastās daļas a b un c d, kurām spēkā ir vienādība: a · d = b · c.

Nevienādas kopīgās frakcijas- parastās daļas a b un c d, kurām vienādība: a · d = b · c nav patiesa.

Vienādu daļskaitļu piemērs: 1 3 un 4 12 – tā kā ir spēkā vienādība 1 · 12 = 3 · 4.

Gadījumā, ja izrādās, ka daļas nav vienādas, parasti ir arī jānoskaidro, kura no dotajām daļām ir mazāka un kura lielāka. Lai atbildētu uz šiem jautājumiem, kopējās daļskaitļus salīdzina, reducējot tos līdz kopsaucējam un pēc tam salīdzinot skaitītājus.

Daļskaitļi

Katra daļa ir daļskaitļa ieraksts, kas būtībā ir tikai “apvalks”, semantiskās slodzes vizualizācija. Bet tomēr ērtības labad mēs apvienojam daļskaitļa un daļskaitļa jēdzienus, vienkārši sakot - daļskaitli.

Visiem daļskaitļiem, tāpat kā jebkuram citam skaitļam, ir sava unikālā atrašanās vieta koordinātu starā: starp daļām un punktiem koordinātu starā ir savstarpēja atbilstība.

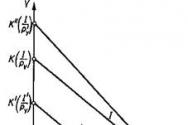
Lai koordinātu starā atrastu punktu, kas apzīmē daļskaitli m n, no koordinātu sākuma pozitīvā virzienā ir jānozīmē m segmenti, kuru katra garums būs 1 n vienības segmenta daļa. Segmentus var iegūt, sadalot vienības segmentu n vienādās daļās.

Kā piemēru norādīsim uz koordinātu stara punktu M, kas atbilst daļai 14 10. Tā posma garums, kura gali ir punkts O un tuvākais punkts, kas atzīmēts ar nelielu domuzīmi, ir vienāds ar 1 10 vienības segmenta daļām. Punkts, kas atbilst frakcijai 14 10, atrodas 14 šādu segmentu attālumā no sākuma.

Ja daļas ir vienādas, t.i. tie atbilst vienam un tam pašam daļskaitlim, tad šīs daļdaļas kalpo kā viena un tā paša punkta koordinātas uz koordinātu stara. Piemēram, koordinātas vienādu daļskaitļu veidā 1 3 , 2 6 , 3 9 , 5 15 , 11 33 atbilst vienam un tam pašam koordinātu stara punktam, kas atrodas trešdaļas attālumā no vienības segmenta, kas izkārtots no sākuma. pozitīvā virzienā.

Šeit darbojas tas pats princips kā ar veseliem skaitļiem: horizontālā koordinātu starā, kas vērsts pa labi, punkts, kuram atbilst lielākā daļa, atradīsies pa labi no punkta, kuram atbilst mazākā daļa. Un otrādi: punkts, kura koordināte ir mazāka daļa, atradīsies pa kreisi no punkta, kuram atbilst lielākā koordināte.

Pareizās un nepareizās daļskaitļi, definīcijas, piemēri

Daļskaitļu dalīšanas pareizajā un nepareizajā pamatā ir skaitītāja un saucēja salīdzinājums vienā un tajā pašā daļskaitlī.

7. definīcija

Pareiza frakcija ir parasta daļa, kurā skaitītājs ir mazāks par saucēju. Tas ir, ja nevienlīdzība m< n , то обыкновенная дробь m n является правильной.

Nepareiza frakcija ir parasta daļa, kuras skaitītājs ir lielāks vai vienāds ar saucēju. Tas ir, ja nedefinētā nevienādība ir izpildīta, tad parastā daļa m n ir nepareiza.

Šeit ir daži piemēri: - pareizās frakcijas:

1. piemērs

5 / 9 , 3 67 , 138 514 ;

Nepareizas frakcijas:

2. piemērs

13 / 13 , 57 3 , 901 112 , 16 7 .

Ir iespējams arī definēt pareizās un nepareizās daļskaitļus, salīdzinot daļskaitli ar vienu.

8. definīcija

Pareiza frakcija– parastā daļa, kas ir mazāka par vienu.

Nepareiza frakcija– parastā daļa, kas vienāda vai lielāka par vienu.

Piemēram, daļskaitlis 8 12 ir pareizs, jo 8 12< 1 . Дроби 53 2 и 14 14 являются неправильными, т.к. 53 2 >1 un 14 14 = 1.

Padziļināsimies, kāpēc daļskaitļi, kuros skaitītājs ir lielāks par saucēju vai vienāds ar to, tiek saukti par “nepareiziem”.

Apsveriet nepareizo daļskaitli 8 8: tā norāda, ka no objekta, kas sastāv no 8 daļām, ir ņemtas 8 daļas. Tādējādi no pieejamajām astoņām akcijām varam izveidot veselu objektu, t.i. dotā daļa 8 8 būtībā atspoguļo visu objektu: 8 8 = 1. Daļskaitļi, kuros skaitītājs un saucējs ir vienādi, pilnībā aizstāj naturālo skaitli 1.

Aplūkosim arī daļskaitļus, kuros skaitītājs pārsniedz saucēju: 11 5 un 36 3. Skaidrs, ka daļskaitlis 11 5 norāda, ka no tā varam izveidot veselus divus objektus un vēl paliek piektdaļa. Tie. daļa 11 5 ir 2 objekti un vēl 1 5 no tā. Savukārt 36 3 ir daļa, kas būtībā nozīmē 12 veselus objektus.

Šie piemēri ļauj secināt, ka nepareizās daļdaļas var aizstāt ar naturāliem skaitļiem (ja skaitītājs dalās ar saucēju bez atlikuma: 8 8 = 1; 36 3 = 12) vai naturāla skaitļa un pareizas daļskaitļa summu. (ja skaitītājs nedalās ar saucēju bez atlikuma: 11 5 = 2 + 1 5). Iespējams, tāpēc šādas frakcijas sauc par “neregulārajām”.

Šeit mēs saskaramies arī ar vienu no vissvarīgākajām skaitļu prasmēm.

9. definīcija

Visas daļas atdalīšana no nepareizas daļas- Šis ir nepareizas daļskaitļa ieraksts kā naturāla skaitļa un pareizas daļskaitļa summa.

Ņemiet vērā arī to, ka pastāv cieša saistība starp nepareizām daļskaitļiem un jauktiem skaitļiem.

Pozitīvās un negatīvās frakcijas

Iepriekš mēs teicām, ka katra parastā daļa atbilst pozitīvam daļskaitlim. Tie. Kopējās frakcijas ir pozitīvas daļskaitļi. Piemēram, daļskaitļi 5 17, 6 98, 64 79 ir pozitīvi, un, ja nepieciešams īpaši uzsvērt daļskaitļa “pozitivitāti”, to raksta, izmantojot plus zīmi: + 5 17, + 6 98, + 64 79.

Ja parastai daļai piešķiram mīnusa zīmi, tad iegūtais ieraksts būs negatīva daļskaitļa ieraksts, un šajā gadījumā mēs runājam par negatīvām daļām. Piemēram, - 8 17, - 78 14 utt.

Pozitīvās un negatīvās daļas m n un - m n ir pretēji skaitļi, piemēram, daļskaitļi 7 8 un - 7 8 ir pretēji.

Pozitīvas daļskaitļi, tāpat kā jebkuri pozitīvi skaitļi kopumā, nozīmē saskaitīšanu, augšupejošu izmaiņu. Savukārt negatīvās daļas atbilst patēriņam, samazinājuma virziena maiņai.

Ja skatāmies uz koordinātu līniju, mēs redzēsim, ka negatīvās daļas atrodas pa kreisi no sākuma punkta. Punkti, kuriem atbilst pretējās daļas (m n un - m n), atrodas vienādā attālumā no koordinātu O sākuma, bet pretējās tā pusēs.

Šeit mēs atsevišķi runāsim arī par daļām, kas rakstītas formā 0 n. Šāda daļa ir vienāda ar nulli, t.i. 0 n = 0 .

Apkopojot visu iepriekš minēto, mēs nonākam pie vissvarīgākā racionālo skaitļu jēdziena.

10. definīcija

Racionālie skaitļi ir pozitīvo daļskaitļu, negatīvo daļskaitļu un formas 0 n daļu kopa.

Darbības ar daļskaitļiem

Uzskaitīsim pamatdarbības ar daļskaitļiem. Kopumā to būtība ir tāda pati kā atbilstošām darbībām ar naturāliem skaitļiem

1. Daļskaitļu salīdzināšana - mēs apspriedām šo darbību iepriekš.
2. Daļskaitļu saskaitīšana - parasto daļskaitļu pievienošanas rezultāts ir parasta daļa (konkrētā gadījumā samazināta līdz naturālam skaitlim).
3. Daļskaitļu atņemšana ir saskaitīšanas reverss, kad nezināmas daļas noteikšanai izmanto vienu zināmu daļu un noteiktu daļu summu.
4. Daļskaitļu reizināšana – šo darbību var raksturot kā daļskaitļa atrašanu no daļskaitļa. Divu parasto daļskaitļu reizināšanas rezultāts ir parasta daļa (konkrētā gadījumā vienāda ar naturālu skaitli).
5. Daļskaitļu dalīšana ir reizināšanas apgrieztā darbība, kad nosakām daļskaitli, ar kuru jāreizina dotais, lai iegūtu zināmo divu daļu reizinājumu.

Ja pamanāt tekstā kļūdu, lūdzu, iezīmējiet to un nospiediet Ctrl+Enter